Машины сургалтанд шугаман регресс

Шугаман регресс бол хамгийн хялбар бөгөөд түгээмэл хэрэглэгддэг Machine Learning алгоритмуудын нэг юм. Энэ нь урьдчилан таамаглах дүн шинжилгээ хийхэд ашигладаг статистикийн арга юм. Шугаман регресс нь борлуулалт, цалин, нас, бүтээгдэхүүний үнэ гэх мэт тасралтгүй / бодит эсвэл тоон хувьсагчдын таамаглалыг гаргадаг .

Шугаман регрессийн алгоритм нь хамааралтай (y) ба нэгээс дээш бие даасан (y) хувьсагчдын хоорондох шугаман холбоог харуулдаг тул шугаман регресс гэж нэрлэдэг. Шугаман регресс нь шугаман харьцааг харуулдаг бөгөөд энэ нь хамааралтай хувьсагчийн утга нь бие даасан хувьсагчийн утгын дагуу хэрхэн өөрчлөгдөж байгааг олж мэдэх болно гэсэн үг юм.

Шугаман регрессийн загвар нь хувьсагчдын хоорондын хамаарлыг илэрхийлсэн налуу шулуун шугамыг өгдөг. Доорх зургийг үзье.

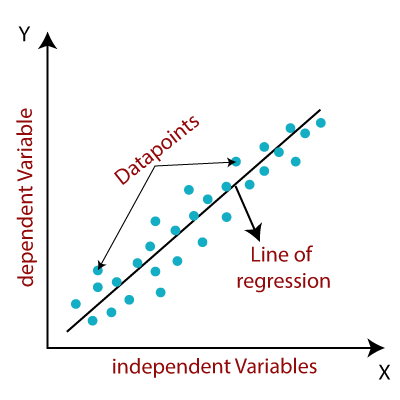
Математикийн хувьд бид шугаман регрессийг дараах байдлаар илэрхийлж болно.

y = a 0 + a 1 x + ε байна

Энд,

Y = Хараат бус хувьсагч (Зорилтот хувьсагч)
X = Бие даасан хувьсах (урьдчилан таамаглах хувьсагч)
a0 = шугамын огтлолцол (нэмэлт эрх чөлөө өгдөг)
a1 = Шугаман регрессийн коэффициент (оролтын утга тус бүрт масштабтай хүчин зүйл).
ε = санамсаргүй алдаа

X ба y хувьсагчийн утга нь шугаман регрессийн загвар дүрслэлд зориулсан сургалтын мэдээллийн өгөгдөл юм.

Шугаман регрессийн төрлүүд

Шугаман регрессийг алгоритмын хоёр төрөлд хувааж болно.

• Энгийн шугаман регресс:
  Хэрэв тоон хамааралтай хувьсагчийн утгыг таамаглахын тулд дан ганц бие даасан хувьсагч ашиглавал ийм шугаман регрессийн алгоритмыг энгийн шугаман регресс гэж нэрлэдэг.
• Олон шугаман регресс:
  Хэрэв тооноос хамааралтай хувьсагчийн утгыг таамаглахын тулд нэгээс олон бие даасан хувьсагч ашигладаг бол Шугаман регрессийн алгоритмыг олон тооны шугаман регресс гэж нэрлэдэг.

Шугаман регрессийн шугам

Хамааралтай ба бие даасан хувьсагчдын хоорондын холбоог харуулсан шугаман шугамыг регрессийн шугам гэж нэрлэдэг . Регрессийн шугам нь хоёр төрлийн харилцааг харуулж чадна.

• Эерэг шугаман харилцаа:
  Хэрэв хамааралтай хувьсагч нь Y тэнхлэгт, бие даасан хувьсагч нь X тэнхлэгт өсөх юм бол ийм харьцааг Эерэг шугаман харилцаа гэж нэрлэнэ.

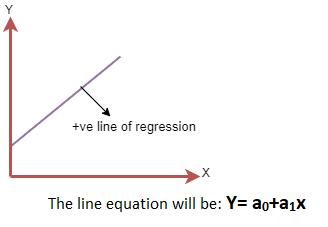
• Сөрөг шугаман харилцаа:
  Хэрэв хамааралтай хувьсагч нь Y тэнхлэг дээр буурч, X тэнхлэг дээр бие даасан хувьсагч нэмэгдэж байвал ийм харьцааг сөрөг шугаман харилцаа гэж нэрлэдэг.

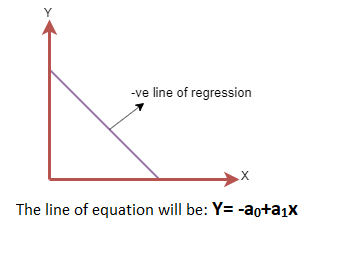
Хамгийн сайн тохирох шугамыг хайж олох:

Шугаман регресстэй ажиллахдаа бидний хамгийн гол зорилго бол хамгийн сайн тохирох шугамыг олох явдал бөгөөд энэ нь урьдчилан тооцоолсон утга ба бодит утгуудын хоорондох алдааг багасгах ёстой гэсэн үг юм. Хамгийн сайн тохирох шугам нь хамгийн бага алдаатай байх болно.

Жингийн өөр өөр утга эсвэл шугамын коэффициент (a ₀ , a ₁ ) нь регрессийн өөр шугамыг өгдөг тул хамгийн тохиромжтой тохирох шугамыг олохын тулд ₀ ба _1- ийн хамгийн сайн утгыг тооцоолох хэрэгтэй. Тиймээс үүнийг бид тооцоолох хэрэгтэй. өртгийн функцийг ашиглах.

Зардлын функц-

• Жингийн өөр өөр утга эсвэл шугамын коэффициент (a ₀ , a ₁ ) нь регрессийн өөр өөр мөрийг өгдөг бөгөөд зардлын функц нь хамгийн сайн тохирох шугамын коэффициентийн утгыг тооцоолоход ашиглагддаг.
• Зардал функц нь регрессийн коэффициент эсвэл жинг оновчтой болгодог. Энэ нь шугаман регрессийн загварыг хэрхэн гүйцэтгэж байгааг хэмждэг.
• Бид оролтын хувьсагчийг гаралтын хувьсагчтай харьцуулж харуулсан зургийн нарийвчлалыг олохын тулд зардлын функцийг ашиглаж болно . Энэхүү зураглалын функцийг Гипотези функц гэж нэрлэдэг .

Шугаман регрессийн хувьд бид дундаж квадрат алдаа (MSE) өртгийн функцийг ашигладаг бөгөөд энэ нь урьдчилан тооцоолсон утга ба бодит утгуудын хооронд гарсан квадрат алдааны дундаж үзүүлэлт юм. Үүнийг дараах байдлаар бичиж болно.

Дээрх шугаман тэгшитгэлийн хувьд MSE-г дараахь байдлаар тооцоолж болно.

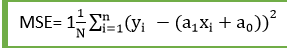
Хаана,

N = Ажиглалтын нийт тоо
Yi = Бодит утга
(a1x _i + a ₀ ) = Урьдчилсан утга.

Үлдэгдэл: Бодит утга ба урьдчилан тооцоолсон утгуудын хоорондын зайг үлдэгдэл гэж нэрлэдэг. Хэрэв ажиглагдсан цэгүүд нь регрессийн шугамаас хол байвал үлдэгдэл өндөр байх тул зардлын функц өндөр байх болно. Хэрэв тараагдсан цэгүүд нь регрессийн шугамтай ойрхон байвал үлдэгдэл нь бага байх тул зардлын функцтэй болно.

Градиент үе:

• Градиент уналт нь өртгийн функцийн градиентийг тооцоолох замаар MSE-г багасгахад ашигладаг.
• Регрессийн загвар нь зардлын функцийг бууруулж шугамын коэффициентийг шинэчлэх зорилгоор градиент түвшинг ашигладаг.
• Энэ нь коэффициентийн утгыг санамсаргүй байдлаар сонгох замаар хийгддэг бөгөөд дараа нь хамгийн бага өртөгтэй функцэд хүрэхийн тулд утгуудыг дахин шинэчлэдэг.

Загварын гүйцэтгэл:

Сайхан байдал нь регрессийн шугам нь ажиглалтын багцад хэр зэрэг нийцэхийг тодорхойлдог. Төрөл бүрийн загваруудаас хамгийн сайн загварыг олох үйл явцыг оновчлол гэж нэрлэдэг . Үүнд дараахь арга замаар хүрч болно.

1. R-квадрат арга:

• R-квадрат бол тохирох чанарыг тодорхойлдог статистикийн арга юм.
• Энэ нь хамааралтай ба бие даасан хувьсагчдын хоорондын харилцааны бат бөх чанарыг 0-100% -ийн масштабаар хэмждэг.
• R-квадратын өндөр утга нь урьдчилан тооцоолсон утга ба бодит утгуудын хоорондох ялгаа бага байгаа тул сайн загварыг илэрхийлнэ.
• Үүнийг тодорхойлох коэффициент буюу олон регрессийн хувьд олон тодорхойлох коэффициент гэж нэрлэдэг .
• Үүнийг дараах томъёогоор тооцоолж болно.

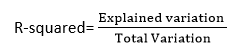
Шугаман регрессийн таамаглал

Шугаман регрессийн зарим чухал таамаглалуудыг доор харуулав. Шугаман регрессийн загварыг бий болгохдоо эдгээр нь албан ёсны шалгалтууд бөгөөд өгөгдсөн мэдээллийн сангаас хамгийн сайн үр дүнд хүрэх боломжийг олгодог.

• Онцлог шинж чанар ба зорилгын хоорондын шугаман хамаарал:
  Шугаман регресс нь хамааралтай ба бие даасан хувьсагчдын шугаман хамаарлыг тооцно.
• Онцлог шинж чанаруудын хоорондох бага эсвэл огт байдаггүй: Олон
  өнцөгт байдал нь бие даасан хувьсагчдын хоорондох өндөр хамааралтай гэсэн үг юм. Олон өнцөгт байдлаас шалтгаалан урьдчилан таамаглагч ба зорилтот хувьсагчдын хоорондох жинхэнэ харьцааг олоход хэцүү байж болно. Эсвэл бид урьдчилан таамаглаж буй хувьсагч нь зорилтот хувьсагч нөлөөлж буйг нь тодорхойлоход хэцүү байдаг гэж хэлж болно. Тиймээс, загвар нь шинж чанарууд эсвэл бие даасан хувьсагчдын хоорондох бага эсвэл огтгүй олон утгыг агуулдаг гэж үздэг.
• Хомосцеастикийн таамаглал:
  Хомосцеастик нь алдааны нэр томъёо нь бие даасан хувьсагчдын бүх утгатай ижил байдаг нөхцөл байдал юм. Хососдестикийн хувьд тархалтын талбайд өгөгдлийг тодорхой хуваарилах загвар байх ёсгүй.
• Алдааны нэр томъёоны хэвийн тархалт:
  Шугаман регресс нь алдааны нэр томъёо нь хэвийн тархалтын хэв маягийг дагаж мөрдөх ёстой гэж үздэг. Хэрэв алдааны нэр томъёог ердийн байдлаар түгээдэггүй бол итгэлцлийн интервал хэт өргөн эсвэл хэт нарийхан байх бөгөөд энэ нь коэффициентийг олоход хүндрэл учруулж болзошгүй юм.
  Үүнийг qq схем ашиглан шалгаж болно . Хэрэв хуйвалдаан нь ямар ч хазайлтгүйгээр шулуун шугамыг харуулсан бол алдаа нь хэвийн тархсан гэсэн үг юм.
• Автокорреляци байхгүй:
  Шугаман регрессийн загвар нь алдааны хувьд автокреляци байхгүй гэж үздэг. Хэрэв алдааны нэр томъёонд ямар нэгэн хамаарал байгаа бол энэ нь загварын нарийвчлалыг эрс бууруулна. Үлдэгдэл алдаануудын хоорондын хамаарал байгаа тохиолдолд автокорреляци ихэвчлэн тохиолддог.