Регрессийн шинжилгээ нь хамааралтай (зорилтот) ба бие даасан (урьдчилан таамаглах) хувьсагчдын нэг буюу хэд хэдэн бие даасан хувьсагчдын хоорондын хамаарлыг загварчлах статистик арга юм. Тодруулбал, Регрессийн шинжилгээ нь хамааралтай хувьсагчийн утга нь бие даасан хувьсагчтай хэрхэн харьцаж өөрчлөгдөж байгааг ойлгоход тусалдаг. Энэ нь температур, нас, цалин, үнэ гэх мэт тасралтгүй / бодит утгыг урьдчилан таамагладаг .
Бид дараах жишгийг ашиглан регрессийн шинжилгээний ойлголтыг ойлгож чадна.
Жишээ: Жил бүр янз бүрийн сурталчилгаа хийдэг, үүнийхээ дагуу борлуулалт хийдэг маркетингийн компани А байна гэж бодъё. Дараахь жагсаалтад компанийн сүүлийн 5 жилийн хугацаанд хийсэн сурталчилгаа болон холбогдох борлуулалтыг харуулав.
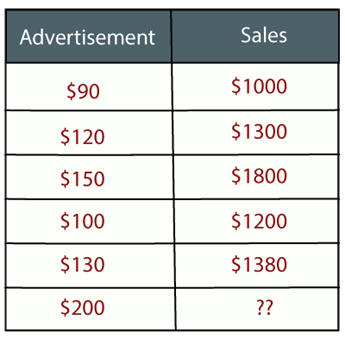
Одоо тус компани 2019 онд 200 долларын сурталчилгааг хийхийг хүсч, энэ жилийн борлуулалтын талаархи таамаглалыг мэдэхийг хүсч байна . Тиймээс машин сурахад ийм төрлийн урьдчилан таамаглах асуудлыг шийдвэрлэхийн тулд регрессийн шинжилгээ хийх шаардлагатай байна.
Регрессийн нь юм хяналттай сургалтын техник хувьсагчдын хоорондын хамаарлыг олоход нь тусалдаг, тасралтгүй гаралт хувьсагч нэг буюу хэд хэдэн шалгуур Хувьсагчууд дээр үндэслэсэн урьдчилан таамаглах боломжийг бидэнд олгодог. Энэ нь голчлон урьдчилан таамаглах, урьдчилан таамаглах, цаг хугацааны цувралыг загварчлах, хувьсагчдын хоорондын учир шалтгааны нөлөөллийн хамаарлыг тодорхойлоход ашигладаг .
Регрессийн хувьд бид өгөгдсөн өгөгдлийн цэгүүдэд хамгийн сайн тохирох хувьсагчдын хоорондох графикийг байрлуулж, энэ схемийг ашиглан машин сургалтын загвар нь өгөгдлийг урьдчилан таамаглах боломжтой болно. Энгийн үгээр хэлбэл "Регресс нь зорилтот-графикийн график дээрх бүх өгөгдлийн цэгүүдээр дамждаг шугам эсвэл муруйг харуулна. Ингэснээр өгөгдлийн цэгүүд ба регрессийн шугамын хоорондох босоо зай хамгийн бага байх болно." Өгөгдлийн цэгүүд болон шугамын хоорондох зай нь загвар нь хүчтэй харилцааг олж авсан эсэхээс үл хамаарна.
Регрессийн зарим жишээг дурдаж болно.
- Температур болон бусад хүчин зүйлсийг ашиглан бороо орохыг урьдчилан таамаглах
- Зах зээлийн чиг хандлагыг тодорхойлох
- Хурдны жолоодлогын улмаас зам тээврийн ослын урьдчилсан таамаглал.
Регрессийн шинжилгээтэй холбоотой нэр томъёо:
- Хараат бус хувьсагч: Урьдчилан таамаглах эсвэл ойлгохыг хүсч буй Регрессийн шинжилгээний гол хүчин зүйлийг хамааралтай хувьсагч гэж нэрлэдэг. Үүнийг зорилтот хувьсагч гэж нэрлэдэг .
- Бие даасан Хувьсах: хамааралтай хувьсагчуудыг нөлөөлж буюу хүчин зүйл хамааралтай хувьсагч бие даасан хувьсагч гэж нэрлэдэг нь мөн гэж нэрлэдэг, утгуудыг урьдчилан таамаглахад ашиглаж байгаа шалгуур .
- Гаднах компани: Outlier нь ажиглагдсан бусад утгуудтай харьцуулахад маш бага эсвэл маш өндөр утгын аль алиныг нь агуулдаг ажиглалт юм. Гадны худалдаачин үр дүнд нь саад учруулж болзошгүй тул үүнээс зайлсхийх хэрэгтэй.
- Multicollinearity: Хэрэв бие даасан хувьсагчид бусад хувьсагчдаас бие биетэйгээ маш их хамааралтай бол ийм нөхцөлийг Multicollinearity гэж нэрлэдэг. Энэ нь хамгийн их нөлөөлдөг хувьсагчийг эрэмбэлэх явцад асуудал үүсгэдэг тул энэ нь мэдээллийн санд байх ёсгүй.
- Дутуу тохирох ба хэт ачаалал: Хэрэв бидний алгоритм нь сургалтын өгөгдлийн сантай сайн ажилладаг боловч тестийн өгөгдлийн системтэй сайн тохирдоггүй бол ийм асуудлыг Overfitting гэж нэрлэдэг . Хэрэв бидний алгоритм нь сургалтын мэдээллийн дататай ч сайн ажиллахгүй бол ийм асуудлыг дутуу дулимаг гэж нэрлэдэг .
Бид яагаад Регрессийн шинжилгээг ашигладаг вэ?
Дээр дурдсанчлан, регрессийн шинжилгээ нь тасралтгүй хувьсагчийг урьдчилан таамаглахад тусалдаг. Бодит ертөнцөд цаг агаарын байдал, борлуулалтын таамаглал, маркетингийн чиг хандлага гэх мэт ирээдүйн талаархи урьдчилсан таамаглал хэрэгтэй янз бүрийн хувилбарууд байдаг бөгөөд ийм тохиолдолд таамаглалыг илүү нарийвчлалтай хийх боломжтой технологи хэрэгтэй болно. Ийм тохиолдолд бидэнд статистикийн арга бөгөөд машин сургалт, мэдээллийн шинжлэх ухаанд ашигладаг регресс анализ хэрэгтэй. Регрессийн шинжилгээг ашиглах өөр бусад шалтгааныг доор харуулав.
- Регресс нь зорилтот болон бие даасан хувьсагч хоёрын хоорондын хамаарлыг тооцдог.
- Энэ нь өгөгдлийн чиг хандлагыг олоход ашиглагддаг.
- Энэ нь бодит / тасралтгүй утгыг урьдчилан таамаглахад тусална.
- Регрессийг хийснээр бид хамгийн чухал хүчин зүйл, хамгийн бага чухал хүчин зүйл, бусад хүчин зүйл тус бүр хэрхэн нөлөөлж байгааг найдвартай тодорхойлж чадна .
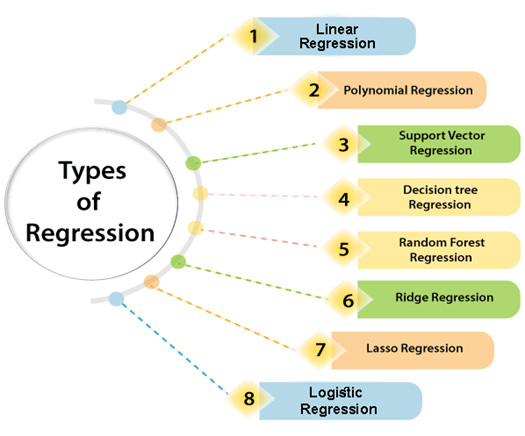
Регрессийн төрлүүд
Мэдээллийн шинжлэх ухаан, машин судлалд ашигладаг төрөл бүрийн регрессүүд байдаг. Төрөл бүр нь өөр өөр хувилбарууд дээр өөрийн гэсэн ач холбогдолтой байдаг боловч үндсэндээ бүх регрессийн аргууд нь бие даасан хувьсагчийн хараат бус хувьсагчийн нөлөөнд дүн шинжилгээ хийдэг. Доор үзүүлсэн зарим чухал регрессийн төрлүүдийг авч үзье.
- Шугаман регресс
- Логистик регресс
- Полиномын регресс
- Вектор регрессийг дэмжинэ
- Шийдлийн модны регресс
- Санамсаргүй ойн нөхөн сэргээлт
- Мөрний регресс
- Лассо регресс:
Шугаман регресс:
- Шугаман регресс гэдэг нь урьдчилан таамаглах шинжилгээ хийхэд ашигладаг статистик регрессийн арга юм.
- Энэ нь регресс дээр ажилладаг, тасралтгүй хувьсагчдын хоорондын холбоог харуулдаг маш энгийн бөгөөд хялбар алгоритмуудын нэг юм.
- Машины сургалтанд регрессийн асуудлыг шийдвэрлэхэд ашигладаг.
- Шугаман регресс нь бие даасан хувьсагч (X тэнхлэг) ба хамааралтай хувьсагч (Y тэнхлэг) хоорондын шугаман холбоог харуулдаг тул шугаман регресс гэж нэрлэдэг.
- Хэрэв зөвхөн нэг оролтын хувьсагч (x) байгаа бол ийм шугаман регрессийг энгийн шугаман регресс гэж нэрлэдэг . Хэрэв нэгээс олон оролтын хувьсагч байгаа бол ийм шугаман регрессийг олон шугаман регресс гэж нэрлэдэг .
- Шугаман регрессийн загвар дахь хувьсагчдын хоорондын хамаарлыг доорх зургийг ашиглан тайлбарлаж болно. Энд бид тухайн ажилтны жилийн цалин хөлсийг тухайн жилийн туршлагаас хамаарч урьдчилан тооцдог .
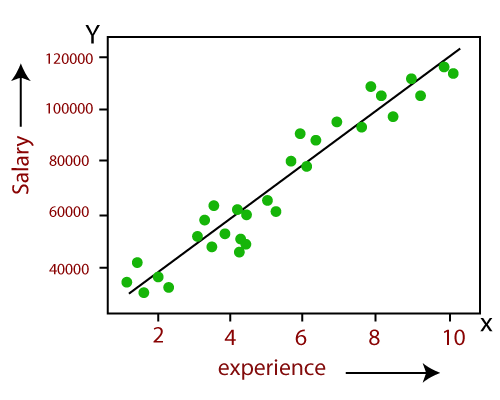
- Шугаман регрессийн математикийн тэгшитгэлийг доор харуулав.
Энд Y = хамааралтай хувьсагчууд (зорилтот хувьсагчид),
X = Бие даасан хувьсагчид (таамаглах хувьсагчууд),
а ба b нь шугаман коэффициент
X = Бие даасан хувьсагчид (таамаглах хувьсагчууд),
а ба b нь шугаман коэффициент
Шугаман регрессийн зарим түгээмэл хэрэглээ нь:
- Хандлага, борлуулалтын тооцоонд дүн шинжилгээ хийх
- Цалингийн урьдчилсан мэдээ
- Үл хөдлөх хөрөнгийн урьдчилсан таамаглал
- Замын хөдөлгөөнд оролцож буй ETA-д ирэх.
Логистикийн регресс:
- Логистик регресс бол ангиллын асуудлыг шийдвэрлэхэд ашигладаг өөр нэг хяналттай сурах алгоритм юм. Онд ангилал асуудал , бид ийм 0 эсвэл 1 зэрэг хоёртын эсвэл салангид хэлбэрээр хамааралтай хувьсагчуудыг байна.
- Логистик регрессийн алгоритм нь 0 эсвэл 1, Тийм эсвэл Үгүй, үнэн эсвэл худал, спам эсвэл спам биш гэх мэт категори хувьсагчтай ажилладаг.
- Энэ нь магадлалын тухай ойлголт дээр ажилладаг урьдчилсан таамаглах алгоритм юм.
- Логистик регресс нь регрессийн нэг төрөл боловч тэдгээрийг хэрхэн ашиглах нэр томъёоны шугаман регрессийн алгоритмаар ялгаатай.
- Логистик регресс нь өртгийн нарийн төвөгтэй функц болох сигмоид функц эсвэл логистик функцийг ашигладаг . Энэхүү сигмоид функцийг логистик регресс дэх өгөгдлийг загварчлахад ашигладаг. Функцыг дараах байдлаар илэрхийлж болно.
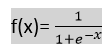
- f (x) = 0 ба 1-ийн хоорондох гарц.
- x = функцэд оруулах
- e = байгалийн логарифмын суурь.
Функцэд оролтын утгыг (өгөгдөл) өгөхөд S-муруйг дараах байдлаар өгнө.
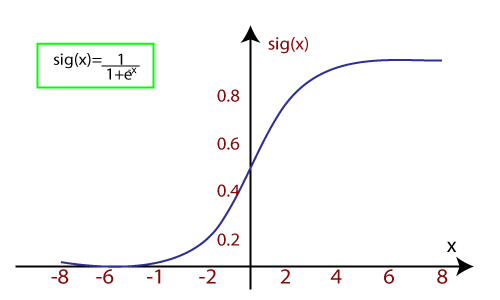
- Энэ нь босго түвшний тухай ойлголтыг ашигладаг бөгөөд босго түвшнээс дээш утгууд нь 1 хүртэлх хэмжээтэй, босго түвшнээс доогуур утгууд 0 хүртэлх хэмжээтэй байна.
Логистик регрессийн гурван төрөл байдаг.
- Хоёртын тоо (0/1, дамжуулалт / амжилтгүй)
- Олон (муур, нохой, арслан)
- Ординаль (бага, дунд, өндөр)
Полиномын регресс:
- Полиномын регресс бол шугаман бус өгөгдлийн санг шугаман загвар ашиглан загварчилсан регрессийн нэг төрөл юм .
- Энэ нь олон шугаман регресстэй төстэй боловч x-ийн утга ба y-ийн харгалзах нөхцлийн утгуудын хоорондох шугаман бус муруйтай таарна.
- Шугаман бус байдлаар байрладаг өгөгдлийн цэгүүдээс бүрдэх мэдээллийн сан байдаг гэж үзье, ийм тохиолдолд шугаман регресс нь тэдгээр мэдээллийн цэгүүдэд тохирохгүй байх болно. Ийм мэдээллийн цэгүүдийг нөхөхийн тулд бидэнд Полиномын регресс хэрэгтэй.
- I n Полиномын регресс, анхны шинж чанаруудыг өгөгдсөн градусын полином шинж чанар болгон хувиргаж дараа нь шугаман загвар ашиглан загварчилдаг. Энэ нь тоон цэгүүдийг полиномын шугамыг ашиглан хамгийн сайн тохируулна гэсэн үг юм.
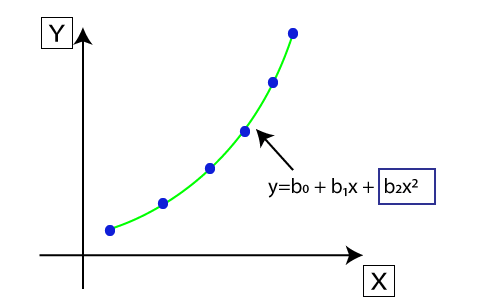
- Y = b 0 + b 1 x шугаман регрессийн тэгшитгэлийг илэрхийлсэн шугаман регрессийн тэгшитгэлээс гаргаж авсан полиномын регрессийн тэгшитгэлийг Y = b 0 + b 1 x + b 2 x 2 + b 3 x 3 + болгон хувиргасан . .... + b n x n байна.
- Энд Y нь урьдчилан тооцоолсон / зорилтот гаралт, b 0 , b 1 , ... b n нь регрессийн коэффициент юм. x нь бидний бие даасан / оролтын хувьсагч юм.
- Коэффициентууд квадраттай шугаман хэвээр байгаа тул загвар нь шугаман хэвээр байна
Тэмдэглэл: Энэ нь олон шугаман регрессээс ялгаатай нь Полиномын регрессийн үед нэг элемент ижил градус бүхий олон хувьсагчийн оронд өөр өөр градустай байдаг.
Вектор регрессийг дэмжинэ:
Дэмжлэгийн вектор машин нь регресс, ангиллын асуудалд ашиглах боломжтой хяналттай сурах алгоритм юм. Тиймээс бид үүнийг регрессийн асуудалд ашигладаг бол үүнийг дэмжих векторын регресс гэж нэрлэдэг.
Дэмжлэгийн векторын регресс бол тасралтгүй хувьсагчуудад ажилладаг регресс алгоритм юм. Доорх хэрэглэгддэг зарим нэг түлхүүр нь дэмжлэг үзүүлэх Вектор регрессийн :
- Цөм: Энэ нь доод хэмжээст өгөгдлийг илүү өндөр хэмжээтэй өгөгдөл рүү оруулахад ашигладаг функц юм.
- Гиперплантер: Ер нь SVM, энэ нь хоёр ангийн хоорондох тусгаарлах шугам боловч SVR-ийн хувьд энэ нь тасралтгүй хувьсагчдыг урьдчилан тооцоолоход тусалдаг бөгөөд мэдээллийн цэгүүдийн ихэнх хэсгийг хамардаг.
- Хилийн шугам: Хилийн шугамууд нь гиперплэйгээс гадна хоёр шугам бөгөөд энэ нь мэдээллийн цэгүүдэд марж үүсгэдэг.
- Дэмжлэгийн векторууд: Дэмжлэгийн векторууд нь гиперплан ба эсрэг анги руу хамгийн ойр байрлах өгөгдлийн цэгүүд юм.
SVR дээр бид хамгийн дээд тал нь гипер онгоцыг тодорхойлохыг хичээдэг бөгөөд ингэснээр тухайн цэг дээр хамгийн их тооны өгөгдлийн цэгүүд хамрагдана. SVR-ийн гол зорилго бол хилийн шугам дахь хамгийн их өгөгдлийн цэгийг тооцох явдал юм. Гиперплантер (хамгийн тохиромжтой шугам) нь хамгийн их тооны мэдээллийн цэгийг агуулсан байх ёстой . Доорх зургийг үзье.
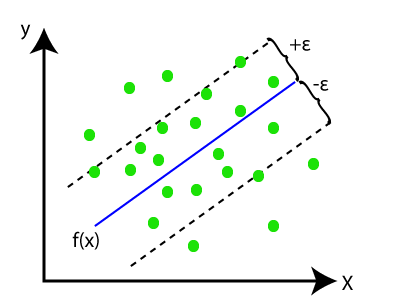
Энд цэнхэр шугамыг гиперплип гэж нэрлэдэг бөгөөд нөгөө хоёр шугамыг хил хязгаар гэж нэрлэдэг.
Шийдвэрлэх модны регресс:
- Шийдвэрлэх мод нь ангилсан болон регрессийн асуудлыг хоёуланг нь шийдвэрлэхэд ашиглаж болох хяналттай сурах алгоритм юм.
- Энэ нь категорийн болон тоон өгөгдлийн аль алинд нь асуудлыг шийдвэрлэх боломжтой
- Шийдлийн модны регресс нь дотоод зангилаа бүр нь шинж чанарын "туршилтыг", салбар бүр нь туршилтын үр дүнг, навчны зангилаа бүр нь эцсийн шийдвэр эсвэл үр дүнг илэрхийлдэг модтой төстэй бүтцийг бий болгодог.
- Шийдвэрийн мод нь зүүн ба баруун хүүхдийн зангилаанд (өгөгдлийн дэд хэсэг) хуваагддаг эх зангилаанаас / эцэг эхийн зангилаанаас (өгөгдлийн сан) үүсдэг. Эдгээр хүүхдийн зангилаа нь цаашид хүүхдийнхээ зангилаанд хуваагддаг бөгөөд өөрсдөө эдгээр зангилааны эцэг эхийн зангилаа болдог. Доорх зургийг үзье.
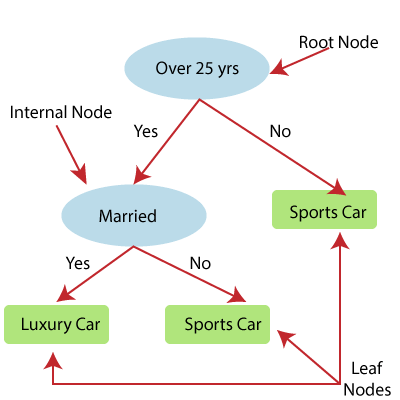
Шийдлийн Tee регрессийн жишээг харуулсан зураг дээрхи энд загвар нь Спорт машин эсвэл Тансаг зэрэглэлийн автомашины хоорондох хүний сонголтыг урьдчилан таамаглахыг оролдож байна.
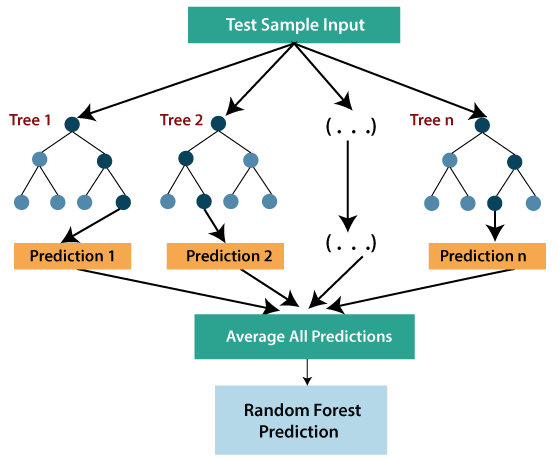
- Санамсаргүй ой бол хамгийн хүчирхэг хяналттай сурах алгоритмуудын нэг бөгөөд регресс болон ангилах даалгавруудыг гүйцэтгэх чадвартай юм.
- Санамсаргүй ойд тохиолддог регресс нь олон тооны шийдвэрийн модыг нэгтгэдэг ансамблийн сургалтын арга бөгөөд модны гарц бүрийн дундаж дээр үндэслэн эцсийн гарцыг урьдчилан таамаглах болно. Хосолсон шийдвэрийн модыг суурь загвар гэж нэрлэдэг бөгөөд үүнийг дараах байдлаар албан ёсоор төлөөлж болно.
g (x) = f 0 (x) + f 1 (x) + f 2 (x) + .... байна.
- Санамсаргүй ой нь нэгтгэсэн шийдвэрийн модыг зэрэгцээ ажиллуулж, бие биетэйгээ харьцахгүй байх ансамблийн сургалтыг Багцлах буюу Ботстрап нэгтгэх аргыг ашигладаг .
- Санамсаргүй ойн регрессийн тусламжтайгаар бид өгөгдлийн сангийн санамсаргүй дэд хэсгийг бий болгосноор загварыг хэт халахаас сэргийлж чадна.
Мөрний сэргэлтийн регресс:
- Мөрний регресс нь шугаман регрессийн хамгийн бат бөх хувилбаруудын нэг бөгөөд бага зэргийн хэвийсэн утгыг нэвтрүүлдэг бөгөөд ингэснээр бид урт хугацааны таамаглал сайжирна.
- Загвар дээр нэмэгдсэн хэвийсэн хэмжээг Ridge Regression торгууль гэж нэрлэдэг . Бид энэ торгуулийн хугацааг lambda-тай үржүүлгийн онцлог тус бүрийн квадрат жинд үржүүлж тооцоолж болно.
- Мөрний регрессийн тэгшитгэл нь:
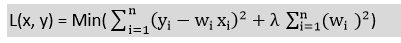
- Бие даасан хувьсагчдын хоорондох өндөр уялдаа холбоо байгаа тохиолдолд ерөнхий шугаман буюу полиномын регресс амжилтгүй болох тул ийм асуудлыг шийдэхийн тулд Ridge регрессийг ашиглаж болно.
- Ridge регресс нь загварчлалын нарийн төвөгтэй байдлыг багасгахад ашигладаг тогтмолжуулалтын арга юм. Үүнийг L2 тогтмолжуулалт гэж нэрлэдэг .
- Хэрэв бид дээжээс илүү олон параметртэй бол асуудлыг шийдэхэд тусална.
Лассо регресс:
- Лассо регресс бол загварын нарийн төвөгтэй байдлыг багасгах өөр нэг тогтмолжуулалтын арга юм.
- Энэ нь торгуулийн нэр томъёо нь дөрвөлжин жингийн оронд зөвхөн туйлын жинг агуулдаг байдгаас бусад нь Риджийн регресстэй төстэй юм.
- Энэ нь үнэмлэхүй утгыг авдаг тул налууг 0 болгож багасгаж болох бол Ridge Regression нь үүнийг зөвхөн 0 болгож багасгаж чадна.
- Үүнийг L1 тогтмолжуулалт гэж нэрлэдэг . Лассо регрессийн тэгшитгэл нь:
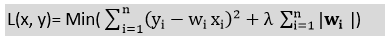
No comments:
Post a Comment