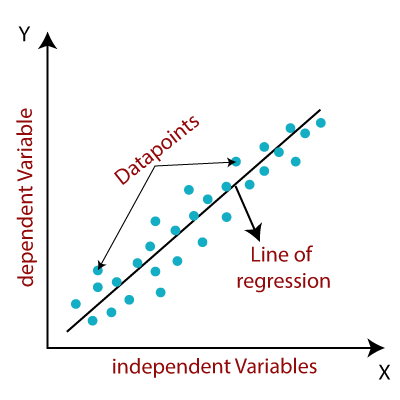
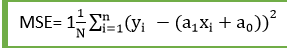Энгийн шугаман регресс гэдэг нь хамааралтай хувьсагч ба дан бие даасан хувьсагч хоёрын хоорондын хамаарлыг загварчилдаг Regression алгоритмын нэг төрөл юм. Энгийн шугаман регрессийн загвараар үзүүлсэн харилцаа нь шугаман буюу налуу шулуун шугам тул түүнийг энгийн шугаман регресс гэж нэрлэдэг.
Энгийн шугаман регрессийн гол цэг бол хамааралтай хувьсагч нь тасралтгүй / бодит утга байх ёстой . Гэсэн хэдий ч бие даасан хувьсагчийг тасралтгүй эсвэл категори утгуудаар хэмжиж болно.
Энгийн шугаман регресс алгоритм нь үндсэндээ хоёр зорилттой байдаг.
- Хоёр хувьсагчийн хоорондын хамаарлыг загварчлах. Орлого зарлага, туршлага, цалингийн хоорондын хамаарал гэх мэт.
- Шинэ ажиглалтуудыг урьдчилан таамаглах. Температурын дагуу цаг агаарын урьдчилсан мэдээ, жилийн хөрөнгө оруулалтын дагуу компанийн орлого гэх мэт.
Шугаман регрессийн энгийн загвар:
Энгийн шугаман регрессийн загварыг дараах томъёогоор ашиглаж болно.
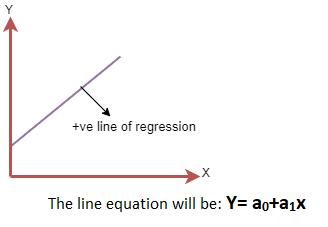
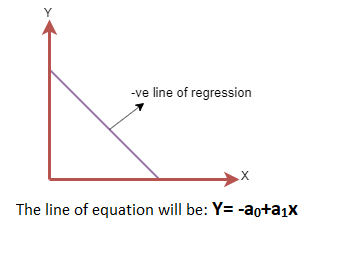
y = a 0 + a 1 x + ε байна
Хаана,
a0 = Энэ нь Регрессийн шугамын огтлолцол юм (x = 0-ийг оруулаад авч болно)
a1 = Энэ нь шугам нэмэгдэж, буурч байгаа эсэхийг харуулсан регрессийн шугамын налуу юм.
ε = Алдааны нэр томъёо. (Сайн загварын хувьд энэ нь үл тоомсорлох болно)
Python ашиглан энгийн шугаман регрессийн алгоритмыг хэрэгжүүлэх
Энгийн шугаман регрессийн асуудлын талаархи жишээ:
Энд бид цалингийн (хамааралтай хувьсагч) ба туршлага (Бие даасан хувьсагч) гэсэн хоёр хувьсагч бүхий мэдээллийн санг авч байна. Энэ асуудлын зорилго нь:
- Эдгээр хоёр хувьсагчийн хооронд ямар нэгэн хамаарал байгаа эсэхийг бид мэдэхийг хүсч байна
- Бид мэдээллийн санд хамгийн тохирох шугамыг олох болно.
- Хамааралтай хувьсагчийг хэрхэн өөрчлөх замаар хамааралтай хувьсагч хэрхэн өөрчлөгдөж байгааг харуулав.
Энэ хэсэгт бид Энгийн шугаман регрессийн загварыг бий болгож, эдгээр хоёр хувьсагчийн хоорондын хамаарлыг илэрхийлэх хамгийн сайн тохирох шугамыг олох болно.
Python-ыг ашиглан машин сурахад энгийн шугаман регрессийн загварыг хэрэгжүүлэхийн тулд бид дараахь алхамуудыг дагаж мөрдөх шаардлагатай.
Алхам 1: Өгөгдлийг урьдчилан боловсруулах
Энгийн шугаман регрессийн загварыг бий болгох эхний алхам бол өгөгдлийг урьдчилан боловсруулах явдал юм. Үүнийг бид энэ зааварт өмнө нь хийж байсан. Гэхдээ дараах алхмуудад өгөгдсөн зарим өөрчлөлтүүд гарах болно.
- Нэгдүгээрт, бид мэдээллийн баазыг ачаалах, графикийн схем, Энгийн шугаман регрессийн загварыг бий болгоход туслах гурван чухал номын санг импортлох болно.
- numpy-г nm гэж импортлох
- импортын MTP гэж matplotlib.pyplot
- pandas-г pd хэлбэрээр импортлох
- Дараа нь бид өгөгдлийн санг манай код руу ачаална.
- data_set = pd.read_csv ( 'Salary_Data.csv' )
Дээрх кодын мөрийг (ctrl + ENTER) ажиллуулснаар Spyder IDE дэлгэц дээрх өгөгдлийн өгөгдлийг хувьсагч хайх сонголтыг дарна уу.
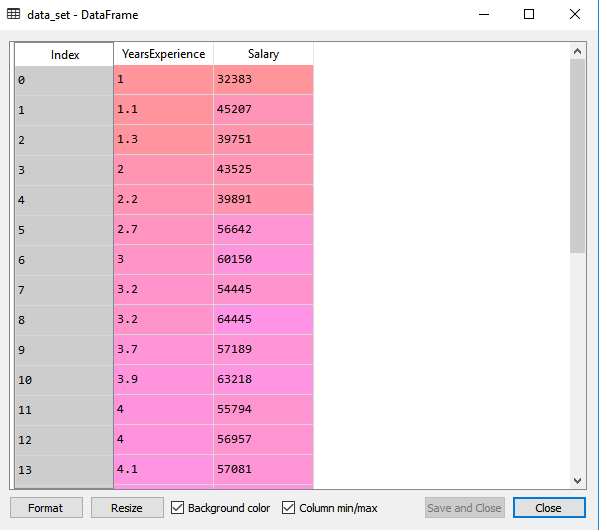
Дээрх үр дүн нь цалингийн болон туршлага гэсэн хоёр хувьсагч бүхий мэдээллийн санг харуулж байна.
Тэмдэглэл: Spyder IDE-д код файлыг агуулсан хавтас нь ажлын директор хэлбэрээр хадгалагдах ёстой бөгөөд мэдээллийн сан эсвэл csv файл нь ижил хавтсанд байх ёстой.
- Үүний дараа өгөгдсөн мэдээллийн баазаас хамааралтай ба бие даасан хувьсагчдыг гаргаж авах хэрэгтэй. Бие даасан хувьсагч нь олон жилийн туршлага бөгөөд хамааралтай хувьсагч нь цалин юм. Үүний код доор байна:
- x = data_set.iloc [:,: - 1 ]. утга
- y = data_set.iloc [:, 1 ]. утга
Дээрх код мөрүүд дээр x хувьсагчийн хувьд бид өгөгдлийн сангаас хамгийн сүүлийн баганыг устгахыг хүссэн тул -1 утга авсан. Y хувьсагчийн хувьд бид 2 утгыг параметр болгон авсан, учир нь хоёрдох баганыг гаргаж авах, индексжүүлэх нь тэгээс эхэлнэ.
Дээрх мөрийн мөрийг ажиллуулснаар X ба Y хувьсагчийн гарцыг дараах байдлаар авна.
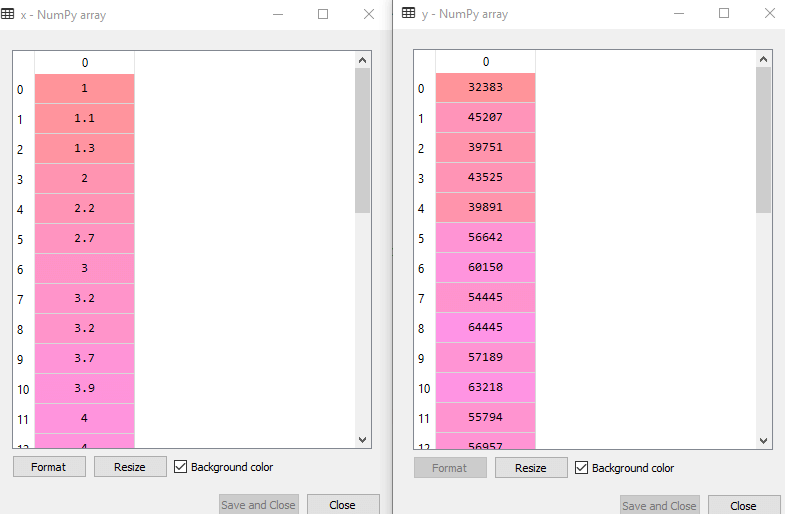
Дээрх гаралтын зурган дээр X (бие даасан) хувьсагчийг харж болох ба Y (хамааралтай) хувьсагчийг өгөгдсөн мэдээллийн баазаас гаргаж авсан болно.
- Дараа нь тестийн ба сургалтын багцад хоёр хувьсагчийг хуваана. Бид 30 ажиглалт хийсэн тул сургалтын багцад 20, тестийн багцад 10 ажиглалт хийх болно. Бид сургалтын өгөгдлийн тусламжтайгаар загвараа сурч, дараа нь загвар өгөгдлийн санг ашиглан загварыг туршихын тулд өгөгдлийн санг хувааж байна. Үүний кодыг доор өгөв.
- # Сургалтын ба тестийн багцад өгөгдлийн санг хуваах.
- sklearn.model_selection импортын галт тэрэг_test_split
- x_train, x_test, y_train, y_test = train_test_split (X, Y, test_size = 1 / 3- , random_state = 0 )
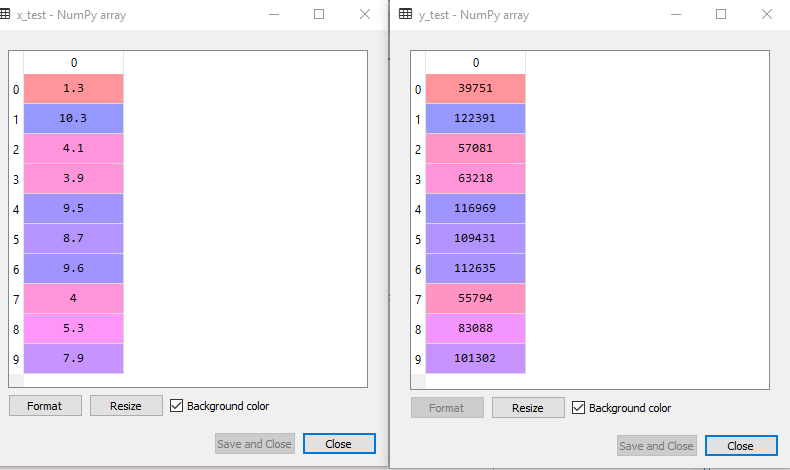
Дээрх кодыг хийснээр бид x-test, x-train, y-test, y-train data-г авах болно. Дараах зургуудыг авч үзье.
Тест-мэдээллийн сан:
Сургалтын мэдээллийн сан:
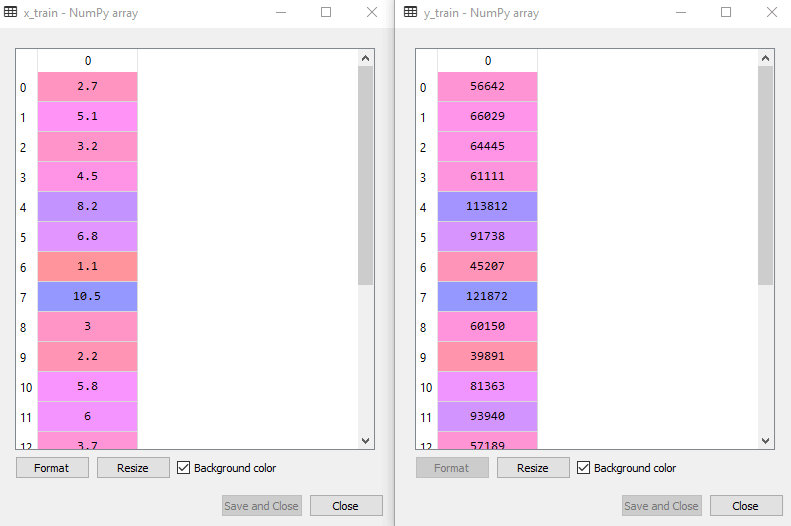
- Энгийн шугаман регрессийн хувьд бид Feature Scaling ашиглахгүй. Python номын сангууд зарим тохиолдолд үүнийг анхаардаг тул энд үүнийг хийх шаардлагагүй болно. Одоо манай мэдээллийн сан түүн дээр ажиллахад бэлэн байгаа бөгөөд өгөгдсөн асуудлын энгийн шугаман регрессийн загварыг эхлүүлэх гэж байна.
Алхам-2: Энгийн шугаман регрессийг сургалтын багцад багтаах.
Одоо хоёрдахь алхам бол манай загварыг сургалтын мэдээллийн санд нийцүүлэх явдал юм. Үүний тулд бид scearit learn- аас linear_model номын сангийн LinearRegression ангиудыг импортолно . Анги импортлосны дараа регрессор нэртэй нэртэй объектыг үүсгэх гэж байна . Үүний кодыг доор өгөв.
- # Энгийн шугаман регрессийн загварыг сургалтын мэдээллийн санд оруулах
- sklearn.linear_model-аас импортын LinearRegression
- регрессор = LinearRegression ()
- regressor.fit (x_train, y_train)
Дээрх кодонд бид энгийн (Linear Regression) объектыг сургалтын багцад тааруулахын тулд fit () аргыг ашигласан. Фит () функцийн хувьд бид хамааралтай ба бие даасан хувьсагчдад зориулсан сургалтын өгөгдлийн сан болох x_train ба y_train-ийг дамжуулсан. Загвар нь урьдчилан таамаглагч ба зорилтот хувьсагчдын хоорондын хамаарлыг хялбархан мэдэж сурахын тулд бид регрессийн объектоо сургалтын багцад суурилуулсан. Дээрх кодын мөрүүдийг гүйцэтгэсний дараа бид дараах гаралтыг авна.
Үр дүн:
Гарч байгаа [7]: LinearRegression (copy_X = Үнэн, fit_intercept = Үнэн, n_jobs = Аль нь ч биш, хэвийн болгох = Худал)
Алхам: 3. Туршилтын үр дүнг урьдчилан таамаглах:
хамааралтай (цалин) ба бие даасан хувьсагч (Туршлага). Тиймээс одоо манай загвар шинэ ажиглалтын үр дүнг урьдчилан таамаглахад бэлэн байна. Энэ алхам дээр бид загвар өгөгдлийг туршилтын өгөгдлийн сан (шинэ ажиглалт) өгөх бөгөөд энэ нь зөв гаралтыг урьдчилан таамаглаж чадах эсэхийг шалгах боломжтой болно.
Бид таамаглал вектор бий болгоно y_pred болон x_pred сургалтын багц туршилтын Датасетийн таамаглал болон урьдчилан тус тус агуулсан байдаг болно.
- # Туршилт ба Сургалтын багц үр дүнг үнэлэх
- y_pred = regressor.predict (x_test)
- x_pred = regressor.predict (x_train)
Дээрх код мөрүүдийг ажиллуулахдаа y_pred ба x_pred гэсэн хоёр хувьсагчийг сургалтын багц болон тестийн багцад зориулагдсан цалингийн урьдчилсан тооцоог агуулсан хувьсагч судлаачийн хувилбаруудад бий болгоно.
Үр дүн:
Та IDE дахь хувьсагчийг судлах сонголтыг дарж хувьсагчийг шалгаж, мөн y_pred ба y_test-ийн утгыг харьцуулж үр дүнг харьцуулж болно. Эдгээр утгуудыг харьцуулж үзвэл манай загвар хэр сайн ажиллаж байгааг шалгаж чадна.
Алхам: 4. Сургалтын үр дүнг төсөөлөх:
Одоо энэ алхамаар бид сургалтын үр дүнг төсөөлөх болно. Үүний тулд бид урьдчилан боловсруулалтын шатанд аль хэдийн импортолсон pyplot номын сангийн scatter () функцийг ашиглах болно. Тархалтын () функц нь ажиглалт нь тарсан газрыг бий болгох болно.
X тэнхлэгт бид ажилчдын олон жилийн туршлагыг, ажилчдын цалингийн тухай у-тэнхлэгийг оруулна. Функцээр бид сургалтын багцын бодит утгыг дамжуулж өгөх болно. Энэ нь жилийн туршлага x_train, сургалтын цалин, сургалтын багц, ажиглалтын өнгө гэсэн үг юм. Энд бид ажиглалтад зориулж ногоон өнгийг авч байна, гэхдээ энэ нь тухайн сонголтын дагуу ямар ч өнгө байж болно.
Одоо бид регрессийн шугамыг зурах хэрэгтэй бөгөөд үүний тулд бид pyplot номын сангийн plot () функцийг ашиглана. Энэ функцээр бид сургалтын багц туршлага, сургалтын багц x_pred, мөрний өнгө зэрэг олон жилийн туршлагыг дамжуулах болно.
Дараа нь, бид талбайн нэрийг өгнө. Тиймээс энд бид pyplot номын сангийн гарчиг () функцийг ашиглаж нэрийг нь ("Цалин, туршлага (Сургалтын мэдээллийн сан )") дамжуулна .
Үүний дараа бид xlabel () ба ylabel () функцийг ашиглан x-тэнхлэг ба y тэнхлэгт шошго өгнө .
Эцэст нь бид дээрх бүх зүйлийг show () ашиглан график хэлбэрээр дүрслэх болно. Кодыг дор өгөв
- mtp.scatter (x_train, y_train, color = "green" )
- mtp.plot (x_train, x_pred, color = "red" )
- mtp.title ( "Цалин, туршлага (Сургалтын мэдээллийн сан" ))
- mtp.xlabel ( "Олон жилийн туршлага" )
- mtp.ylabel ( "Цалин ( Рупийд )" )
- Mtp.show ()
Үр дүн:
Дээрх кодын мөрүүдийг гүйцэтгэснээр бид дараахь график схемийг үр дүн болгож авна.
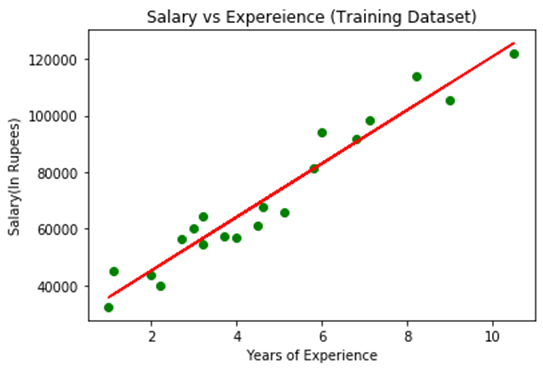
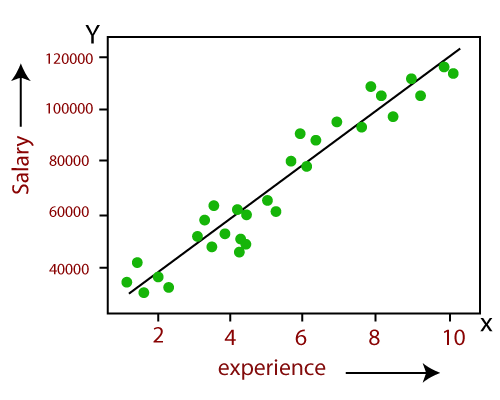
Дээрх зураг дээр бид бодит цэгүүдийн ажиглалтын цэгүүдийг ногоон цэгүүд болон урьдчилан тооцоолсон утгыг улаан регрессийн шугамаар бүрхэж байгааг харж болно. Регрессийн шугам нь хамааралтай ба бие даасан хувьсагчийн хоорондын хамаарлыг харуулж байна.
Шугамын зөв тохирох байдлыг бодит утга ба урьдчилан таамагласан утгуудын хоорондын зөрүүг тооцоолж ажиглаж болно. Гэхдээ дээр дурьдсан зургаас харахад ажиглалтын ихэнх нь регрессийн шугамд ойрхон байгаа тул манай загвар сургалтын багцад тохирсон байдаг.
Алхам: 5. Тестийн үр дүнг төсөөлөх:
Өмнөх алхам дээр бид загварынхаа гүйцэтгэлийг сургалтын багц дээр дүрслэн харуулсан болно. Одоо бид Тестийн багцад зориулж ижил зүйлийг хийх болно. Бүрэн код нь дээрх кодтой адил хэвээр байх болно, үүнээс бусад тохиолдолд бид x_train ба y_train-ийн оронд x_test, y_test-ийг ашиглах болно.
Энд бид ажиглалт, регрессийн шугамын өнгийг хоёр талбайн хооронд ялгахын тулд өөрчилж байгаа боловч энэ нь заавал биш юм.
- # Тестийн үр дүнг # үзүүлэх
- mtp.scatter (x_test, y_test, color = "blue" )
- mtp.plot (x_train, x_pred, color = "red" )
- mtp.title ( "Цалин, туршлага (Туршилтын мэдээллийн сан" ))
- mtp.xlabel ( "Олон жилийн туршлага" )
- mtp.ylabel ( "Цалин ( Рупийд )" )
- Mtp.show ()
Үр дүн:
Дээрх мөрийн мөрийг ажиллуулснаар үр дүнг дараах байдлаар авна.
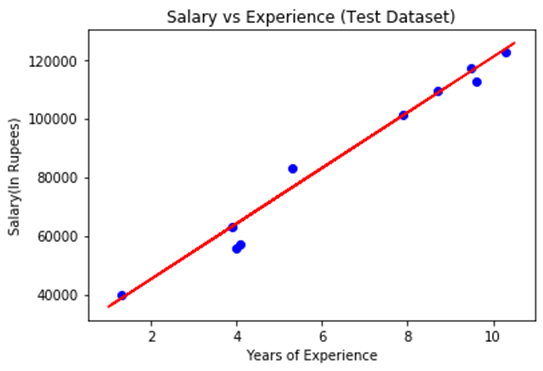
Дээрх зураг дээр цэнхэр өнгөний талаархи ажиглалтууд байдаг бөгөөд урьдчилсан мэдээг улаан регрессийн шугамаар өгдөг. Бидний харж байгаагаар ажиглалтын ихэнх хэсэг нь регрессийн шугамтай ойрхон тул бидний Энгийн шугаман регресс бол сайн загвар бөгөөд сайн таамаглал гаргах чадвартай гэж хэлж болно.